为了帮助大家更加从容地迎接GRE新版考试，拿到心仪的分数。小编为大家总结了一些GRE数学中常用的快速解题技巧。面我们就具体来看一看吧!

　　整体意识

　　有一类题目，题干中涉及到多个未知数，所问的内容也包含多个未知数。这时候就要注意：把多个未知数当作整体求解，往往比分别求解省时很多。

　　【例题】

　　If 5x-3y=7 and 2y-4x=3, then 2x-2y =

　　A.-4 B.4 C.8 D.16 E.20

　　【解析】

　　很多同学看到题目以后，心想：二元一次方程联立求解x和y的值，太简单了，于是开始了疯狂计算。但是，仔细观察题干中的两个式子不难发现：它们相加以后的值就是x-y。

　　因此，我们可以直接将题干中两个式子相加，得到x-y=10，所以2x-2y=20，选择E选项。

　　小编提示：看到题干中的式子不要着急求解未知数的值，观察问题是否和已知条件之间存在关系，利用"整体意识"快速求解。

　　画图求解

　　在部分GRE数学的几何题目中，有一些题目只给出了文字描述而没有给出图形，为了快速且准确地解出此类问题，我们需要简单画图帮助自己解题。

　　【例题】

　　If a right triangle has area 28 and hypotenuse 12, what is its perimeter?

　　A. 20 B.24 C.28 D.32 E.36

　　【解析】

　　这道题目描述了直角三角形的面积为28，斜边为12，让我们求它的周长。因为是纯文字描述，我们可以画个简图辅助求解。

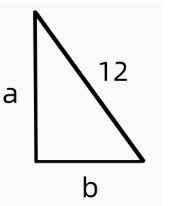
　　根据勾股定理，a^2+b^2=12*12，根据三角形面积公式1/2*a*b=28。

　　根据完全平方公式，我们可以知道(a+b)^2=a^2+b^2+2ab=144+112=256。

　　因此a+b=16，三角形的周长就是a+b+12=28，选择C选项。

　　小编提示：如果几何体只用文字描述而没有给出图形，自己画一个简单图形不仅有助于快速解题，更有助于提高做题的正确率。

　　化繁为简

　　化繁为简主要可以应用在求阴影部分面积的题目中，核心思想是把不不规则的形状通过重新拼接变成规则的形状。

　　【例题】

　　Each of the four semicircles shown in the figure has a side of the square as its diameter and has exactly one point in common with the larger circle. If each side of the square has length 4, what is the sum of the areas of the shaded region?

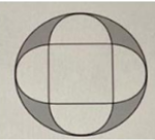
　　A.8π-16 B.12π-16 C.14π-16 D.16π-16 E.18π-16

　　【解析】

　　我们只需要把白色的四个半圆看成一个完整的圆，就可以快速得出阴影部分的面积就等于大圆面积-正方形面积-小圆(四个半圆)面积。

　　根据题目给出的条件及圆面积公式不难求出本体的正确答案B。

　　小编提示：复杂图形通常都可以通过裁减+重新组合拼装成规则图形，大家在解题时要多注意观察，化繁为简。

　　坐标系辅助

　　有些涉及到平面直角坐标系的题目，如果只通过文字解题不够直观，可以画一个坐标系辅助解题。

　　【例题】

　　In the xy-plane, line m passes through the point (7, 7) and is perpendicular to the line x+y =4. The point (a,b) is on line m and is halfway between the point (7, 7) and the line x+y=4. What is the value of a+b?

　　A. 8 B. 9 C. 10 D. 11 E. 12

　　【解析】

　　根据题目描述，我们可以画出下图，并求出线m为y=x，且与线x+y=4的交点为(2,2)。题目说点(a,b)是点(2,2)和(7,7)的中点，因此，a=(2+7)/2，b=(2+7)/2，a+b=9，选择B选项。

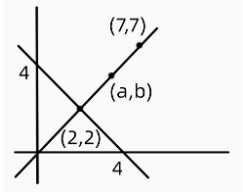
　　小编提示：借助平面直角坐标系解题也是非常常用并且实用的方法，在读到抽象题目时，大家一定要注意画图辅助思考，从而提高解题速度及正确率。