要说A-Level中有哪些学科让人又爱又恨,物理敢称第二,应该就没有其他科目敢称第 一了。物理作为A-Level热门的学科之一,同时也是包括G5院校在内的很多英国顶 尖学府要求的必考科目,下面是由锦秋A-Level物理讲师带来的学术相关内容分享对物理感兴趣的同学一定不要错过哟~
· 分辩率为什么跟波长有关?·
首先,我们需要了解所谓分辨率(Resolution)指的到底是什么。在我们使用仪器测量某个特定物理量的时候,由于仪器上的刻度是固定的,当我们的测量量值正好位于某两个刻度之间的时候,我们会将最终的读数归到某一个特定的刻度上(在某些课程中可能是估读一位),对于一些细微差别,如果其数值小于连续的两个刻度之间的差,那么该仪器可能无法分辨这种细微的差别。举个例子来说,如果两支铅笔的长度分别为100.3毫米和100.4毫米,那么如果我们使用一把普通的尺子(图1.)测量,最终的结果都会是100毫米,这个0.1毫米的差距就被忽略掉了。

图1.普通⽶尺
也就是说,由于这把尺子的分辨率是1毫米,那么小于1毫米的差距就有可能无法被分辨出来。类似的,因为螺旋测微仪(图2.)的分辨率是0.01毫米,所以当测量两个差值为0.1毫米的直径时,螺旋测微仪可以轻易分辨出差别,但是如果处理的直径差值不到0.01毫米的话,那么这种仪器可能就没有办法分辨出差别来了。

图2.螺旋测微仪
同学们在做脉冲回波(Pulse-Echo)定位问题的时候可能遇到过类似这样的问题:对于同样是利用超声波来规避障碍物或者捕捉猎物的海豚和蝙蝠来讲,究竟谁才能够拥有更更好的分辨率呢?这里的分辨率指的是这两种动物在利用脉冲回波判断距离的时候他们能够分辨出的最小距离。在评分方案(Mark Scheme)给出的答案中,波长是一个重要的判断标准,在海 水中的声音速度远大于空气中的声音速度,并且由于题目中假设了两种动物的超声波拥有相同的频率,那么根据公式"v = f λ,我们可以得知蝙蝠的超声波拥有更短的波长(Wavelength,λ),进而判断说蝙蝠拥有更高的分辨率,可以观察到距离上的更细微的变化。
相信不少同学对这个答案存有疑问,为什么波长对测量的分辨率会产生影响呢?这个结论是一系列复杂的理论和公式结合的产物,如果想要得到最严谨的答案,需要的知识远超我们现在学习的范围,所以在这里,我们只做一些近似的或者类比性的说明,如果感兴趣的话,大家还可以自己去查找一些资料来加深对这一知识点的理解。
举个例子,想象一个游泳池当中有一个波长为1米的水波在前进,有一个很细的杆子竖在游泳池中(图3.), 水波此时会毫无阻碍的通过这根细杆,几乎没有任何的反射波产生,也就没办法通过检测反射波来获细杆有关的信息。但是如果前进的水波遇到的是一堵墙,那么就会产生明显的反射波,这堵墙的位置信息也就可以通过这些反射波来推断了。
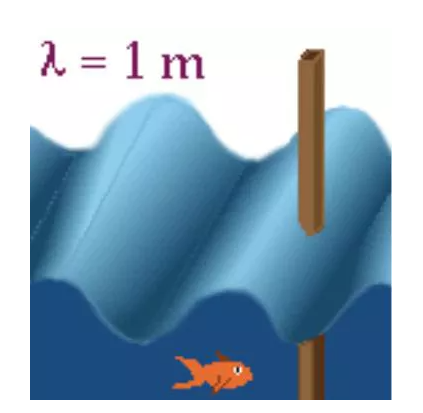
图3.游泳池中的细杆
同学们可以这样理解,如果波长大于或者接近障碍物的尺寸,由于发生了衍射,波会绕开障碍物,很多能量会通过衍射继续传播,但是如果波长远小于障碍物,反射的能量占了主导,那么通过检测这些反射波我们就可以得到跟障碍物距离相关的信息。
所以说,在脉冲会波定位中,波长对于分辨率是有非常大影响的,一般来讲,我们会认为能够分辨的最小距离"d和波长"λ之间呈现线性关系,即"d ∝ λ,也就是说,越小的波长支持我们区分越小的距离差别,这也就是为什么蝙蝠相对于海豚,在假设了他们的超声波频率一样的情况下,蝙蝠会拥有更高分辨率的原因了。
让我们再来看一个在成像方面的应用,先复习一下衍射(Diffraction)相关的知识点,衍射是当一束波在绕过一个障碍物或者通过一个缝隙的时候,如果波长和障碍物大小或者缝隙的宽度接近,那么波就会扩散开来。同时,由于波的叠加原理,衍射后扩散出去的波有可能与其它的波相遇并叠加, 比如当一束波在穿过一个小孔的时候,单缝干涉的现象(图4.)就产生了。

图4.单缝衍射
也就是说,如果一束可见光波穿越了一个圆孔之后投影在屏幕上,那么屏幕上的光应该是中间正对着圆孔的位置最强,但是由于衍射的原因,在其他位置也有一定的强度, 而这些强度会受到衍射强弱的影响,当圆孔的直径远远大于光的波长的时候,衍射现象不明显,投影的光强就会比较集中。但是如果圆孔的尺寸减小到和光的波长接近,那么衍射现象就会变得比较明显,投影出来的光强则会变得不那么集中(图5.)。
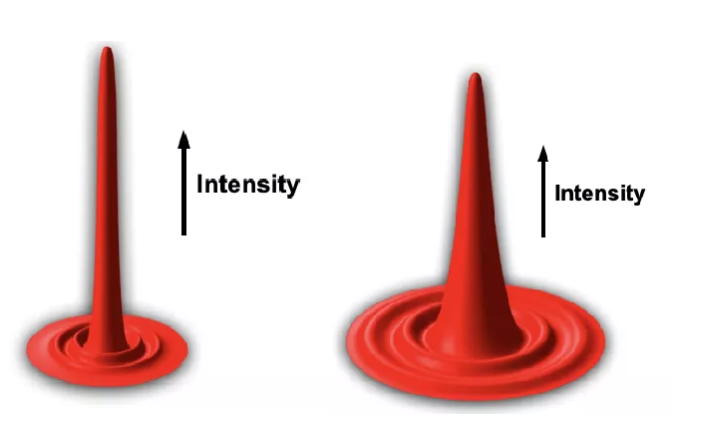
图5. 弱衍射vs强衍射
另外,波是可以进行叠加的,所以如果有两个间距比较近的小孔,波在穿越他们之后又发生了比较明显的衍射现象(图6.),那么衍射波会进行叠加, 而一但发生了叠加,两个小孔之间的波强度会增强,这样小孔之间的界限就会变得模糊起来(图7.)。

图6.多个小孔衍射
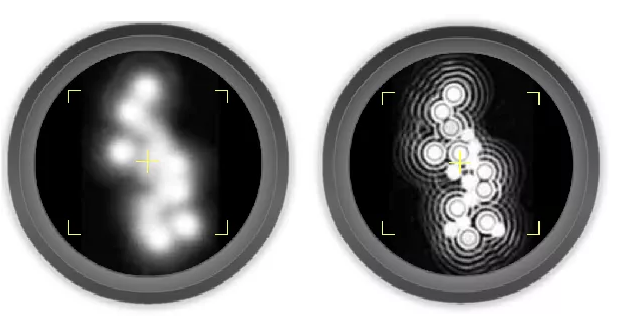
图7.模糊vs清晰的图像
光学显微镜使用可见光成像,其波长范围为380nm - 700nm,当我们观察的样本尺寸约等于甚至小于最小的紫光波长380纳米的时候,衍射现象就会比较明显,图像将会不可避免的变得模糊起来,最终过近的两点将无法被分辨,也就意味着光学显微镜存在有一个不可超越的分辨率,为了实现对更小的样本的观测,需要使用电子显微镜。根据量子理论的相关内容,德布罗意波长可以通过公式"λ = h /p来进行计算,其中h为普朗克常数, 而p为动量。对于高速运动的电子来讲,其波长"λ可以远远小于可见光的最小波长,所以如果使用高速电子来替代可见光作为探测物质的波,理论上我们就可以获得小于380nm的分辨率,这也就解释了为什么电子显微镜可以看见更小的,纳米级别的物体了。
(作者:王培琪)